거듭제곱 꼴 분포(power law distribution; P(x) ~ x^(-α))의 지수(α)를 구하는 방법에는 여러 가지가 있는데 로그 묶기(logarithmic binning; log bin) 방법을 소개(?)한다.
먼저, 묶기(binning) 방법은 다음과 같다: 일반적으로 (x_i, y_i)라는 순서쌍들이 있다고 하자. x_i는 i에 따라 커진다고 하자. 2차원 좌표평면 위의 점들을 생각하면 쉽다. 여기서 x축을 일정한 간격으로 나누고 각 구간의 한가운데 위치를 x_k라고 하자. 각 구간 안에 있는 점들의 y_i의 평균을 구해 y_k라고 한다. 즉 (x_i, y_i)들로부터 (x_k, y_k)를 얻는 과정이다. x축의 각 구간의 길이를 묶는 크기(bin size)라고 한다.
그럼 로그 묶기는 무엇인가. x축을 일정한 간격으로 나누는 대신 이번에는 묶는 크기가 k에 따라 지수함수적으로 증가하는 경우다. 예를 들어, x축을 [1,2), [2,4), [4,8), [8,16) 등으로 나눈다. (모든 x_i가 1 이상이라고 하자.) 이 경우 묶는 크기는 1, 2, 4, 8로 증가한다. 그리고 각 구간에서 y_i의 평균을 구해 역시 (x_k, y_k)를 얻는다. 여기서 x_k는 앞의 방법대로 하면 각각 1.5, 3, 6, 12가 된다.
그런데 로그 묶기에서 y_i의 평균을 구하는 방법에는 두 가지가 있을 수 있다. 하나는 각 구간의 y_i의 합을 그 구간에 포함된 점의 개수로 나누는 것이고 다른 하나는 각 구간의 y_i의 합을 그 구간의 길이(예를 들어, 구간 [4,8)의 길이는 4이다)로 나누는 것이다.
x_i가 자연수이고 y_i는 모두 0보다 큰 값이라고 하자. 즉 y_i = 0인 점은 배제되어 있다. 이 점을 '한 개의 점'으로 처리할 것인지 아닌지에 따라 위 두 방법의 차이가 발생한다. 한 개의 점으로 간주하면 구간의 길이는 곧 그 구간에 포함된 점의 개수이므로 위 두 방법에 차이는 없다. 이 점을 무시하면 구간의 길이보다 점의 개수가 작아져서 점의 개수로 나누어 얻은 y_k가 더 큰 값을 갖는다.
아래 그림에서 raw라고 표시된 빨간 색 선은 지수가 2.5인 거듭제곱 분포를 클로짓 등의 방법을 이용하여 만들어본 것이다. number로 표시된 녹색은 y_i의 합을 점의 개수로 나눈 것이고 length로 표시된 파란 색은 y_i의 합을 구간의 길이로 나눈 것이다.
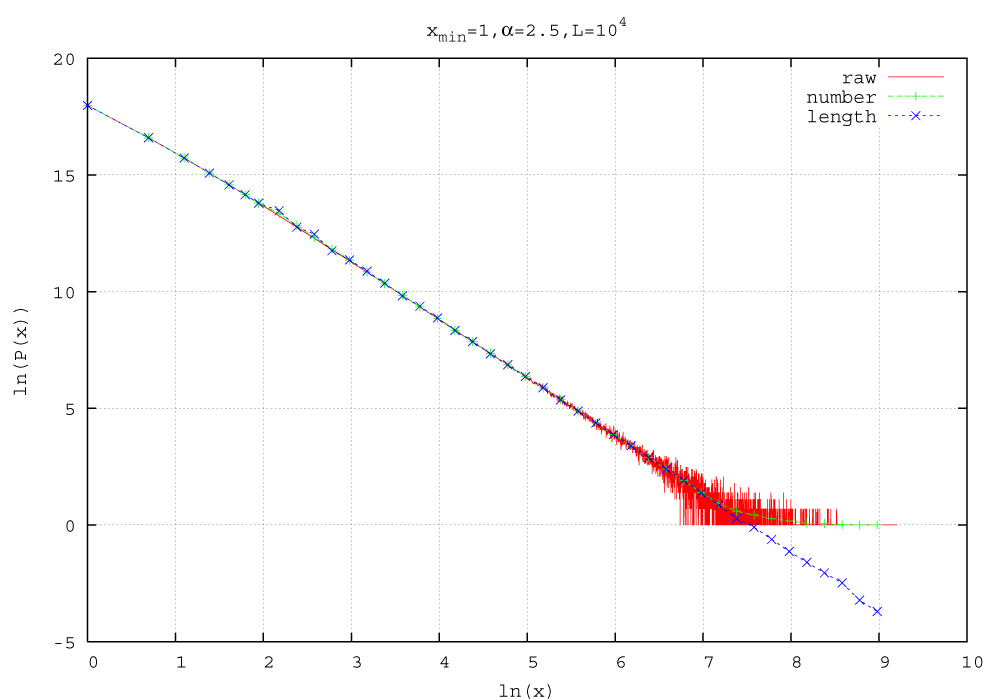
클릭해서 보세요.
빨간 색은 y_i = 0인 경우를 제외하고 얻은 점들을 나타내는데 얼핏 보면 점의 개수로 나눠서 얻은 녹색이 원래 데이터를 더 잘 반영하는 것 같다. 하지만 y_i = 0인 경우를 제외한 것은 순전히 데이터 파일의 크기를 줄이기 위한 나의 편의를 위해서였을 뿐이며 실제로는 그 점들도 고려되어야 하는 게 맞는 것 같다. 결론적으로 구간의 길이로 나눠주는 게 옳다고 생각한다.
이렇게 로그 묶기로 얻은 두 결과를 적절한 구간을 잡아서 직선으로 맞추어보면 구간의 길이로 나누어준 경우 α는 2.491로 원래 값인 2.5에 가깝게 나오고, 점의 개수로 나누어준 경우는 2.477로 앞의 경우보다 덜 맞는 결과가 나온다. 알고나면 별 거 아닌데 둘 사이에 어떤 차이가 있을지를 한참을 고민했더랬다. 끝.
---
2008년 2월 25일 오후 11시 40분 덧붙임.
- 위의 경우에는 구간의 길이로 나누어줄 때 원래 데이터를 더 잘 반영하는 것으로 보이는데 이건 이 데이터의 특수한 경우일 수 있다. 일단 위의 결론은 보류.

