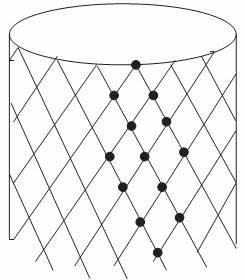
가로로는 주기적 경계조건이며 세로로는 위에서 아래로 모래알이 방향성을 갖고 굴러내린다. 맨 위줄에만 모래알을 하나씩 떨어뜨리고 각 자리(site)의 모래알의 개수가 2개면 무너지기(toppling)가 일어나는데 아래줄 왼쪽 자리와 오른쪽 자리에 모래알을 하나씩 전달하는 식이다. 왼쪽 그림은 하나의 사태(avalanche)의 예를 보인 것으로서, 사태의 왼쪽 경계와 오른쪽 경계가 시간에 따라(즉 아래로 내려오면서) 만나면서 사태가 끝난다는 것을 알 수 있다. 한 가지 가정을 하면, 각 자리에 모래알이 1개 있을 확률과 없을 확률이 모두 1/2라고 한다. 이러면 사태의 경계가 왼쪽으로 또는 오른쪽으로 움직이는 확률도 각각 1/2이며 이는 곧 마구잡이 걷기로 이해할 수 있다.
사태가 시작된 자리에서 두 개의 마구잡이 걷기(RW)가 출발하여 다시 만날 때까지 걸리는 시간은 곧 사태의 지속시간(duration; T)으로 정의되고 사태를 이루는 자리의 개수는 사태의 크기(size; S)로 정의된다. S와 T의 분포를 구하는 것이 목표이며 RW의 결과를 이용하면 된다.
방향성 있는 2차원 모형이지만 세로 방향을 시간축으로 본다면 1차원 위의 RW 문제로 본떠서(mapping) 이해할 수 있다. 즉 원점을 출발한 RW가 시간이 t만큼 흘렀는데도 원점으로 돌아오지 않을 확률을 생존확률(survival probability)로 부르고 1차원에서 이 확률은 t^(-1/2)가 된다.
Pr(T > t) ~ t^(-1/2)
t로 미분하면, Pr(T = t) ~ t^(-3/2)이므로 지속시간 분포의 거듭제곱 지수는 3/2이다.
시간 t 동안 사태의 모양을 보면 세로축으로는 t만큼, 가로축으로는 t^(1/2)만큼의 길이를 가지므로 사태의 크기 s는 t^(3/2)에 비례하며 다시 쓰면 t ~ s^(2/3)이다.
Pr(T > t) ~ Pr(S > s) ~ s^(-1/3)
그러므로 Pr(S = s) ~ s^(-4/3)이며, 사태 크기 분포의 거듭제곱 지수는 4/3이라는 것을 알 수 있다. 끝.

