오... 내 블로그의 글 제목 중에 가장 선정적이라는...
다름이 아니라 이번 <시사IN> 21호에 난 기사 중 전국 아파트 실거래가 자료를 조사한 내용이 있었다. 그림을 보니 이건 딱 거듭제곱 분포로 보이는 것이다!! 그런데 전체 자료(무려 94만여 건)가 당연히 잡지에 다 나올 수는 없고 상위 100등까지는 기사에 표로 나와 있었다. 표 제목은 '대한민국 100대 최고가 아파트'. 그래서 거듭제곱 꼴인지 확인하고 지수를 구해보기로 했다.
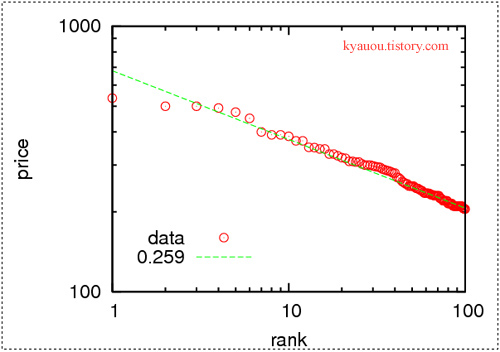
위 그림을 보면, 각 점의 가로축은 등수(즉 1등부터 100등까지)이고 세로축은 아파트 거래가격(단위 천만원)이다. 두 축을 모두 로그로 그렸더니 대충 데이터들이 직선 위에 놓인다. 이는 곧 등수와 가격의 관계가 거듭제곱 꼴(power law)임을 의미한다. 물론 엄밀하게 말하려면 펼쳐진 지수함수(stretched exponential)인지, 로그노멀(log-normal) 분포인지를 다 테스트해봐야 하지만 일단 거듭제곱 꼴로 맞추어(fitting) 봤다.
위에서 보듯이 대충 지수가 -0.259인 직선으로 잘 맞는다. n번째 아파트의 가격을 v_n이라고 하면 v_n ~ n^(-0.259) 라는 말이다. 아파트 가격의 분포가 거듭제곱 꼴이라고 가정하면, 이 결과로부터 아파트 가격 분포의 거듭제곱 지수도 얻을 수 있다. 답은 1 + 1 / 0.259이며 대략 4.86이다. [1] 다시 말해서 아파트 가격을 v라 하면 P(v) ~ v^(-4.86)이라고 할 수 있다. 사실 지수가 4보다 커지면 거듭제곱 꼴보다는 지수함수에 가깝다고 보는 게 맞을 것이다.
결론적으로 아파트 가격 상위 100등에 대해서만 보면 가격 분포에 두꺼운 꼬리(fat tail)는 크게 드러나지 않는 듯 하다.
[1] N개의 아파트 가격들을 크기가 큰 순서대로 일렬로 배열하자. v_1 ≥ v_2 ≥ ... ≥ v_n ≥ ... ≥ v_N이다. 그리고 이 가격들의 분포가 p(v) ~ v^(-α)와 같은 거듭제곱 꼴이라고 하자. v_n은 위의 배열에서 n번째에 나타난다는 조건을 이용하면, N ∫_{v_n~∞} dv p(v) = n라고 쓸 수 있다. 여기 p(v)에 v^(-α)를 넣고 v_n과 n의 관계만 뽑아내면 v_n ~ n^(-1/(α-1))임을 알 수 있다. 위의 경우 1/(α-1) = 0.259이므로 α도 곧바로 얻을 수 있다.
---
시간이 남아서;;;가 아니라 요즘 거듭제곱 분포의 지수를 구하는 프로그램을 짜고 이용해보는 중이라서 한 번 적용해봤다.라고 변명을...

