오늘 낮에 정리한 결과를 올립니다.
접촉 과정에 굳은 무질서(quenched disorder)를 도입하면 임계점이 변하는 것은 물론이고 그리피스 상태와 같은 새로운 상태가 나타나며, 기존의 거듭제곱 꼴과는 다른 '활성화된 눈금잡기' 따위가 보이기도 한다는 얘기를 계속 해왔습니다. 이 주제를 간단히 무질서한 접촉 과정(DCP)이라고 하죠.
앞에 한 얘기를 보기 좋게(?) 그려놓은 게 'DCP의 상그림'이라는 글이었습니다. 그리고 각각의 상태나 임계점에서 시스템이 시간에 따라 어떻게 변하는지, 즉 동역학적 특징이 뭔지도 소개한 적이 있죠. 보이타와 디키슨의 2005년 PRE 논문에서 보인 시늉내기 결과 중 일부를 제가 직접 다시 돌려서 얻은 결과도 보여드린 적이 있습니다.
보이타와 디키슨의 논문에 있던 다른 그림들도 일부만 다시 그려봤습니다. 논문에서 돌린 정도로 많이 돌린 건 아니었구요, 흉내만 낼 수 있는 정도입니다. 지금부터 보려는 동역학적 특징이 뭘 보려는 건지 다시 간단히 얘기하면요, 격자 위의 각 자리에 입자들이 모두 놓여있고 각 입자는 옆의 빈자리에 자신을 복제하거나 사라집니다. 복제율이 낮으면 자연히 입자의 개수가 줄어들겠죠. 특히 '더러운 임계점'보다 낮은 복제율의 경우, 어떻게든 입자는 모두 사라지게 되어 있습니다. 그런데 어떻게 사라지느냐.하는 그 특성이 복제율에 따라 다르다는 겁니다.
DCP의 상그림과 각 복제율에 따른 동역학적 특성을 정리해놓은 제 다른 글들을 보시면, 복제율이 커지면서 깨끗한 임계점을 지나 그리피스 상태가 되고 더러운 임계점을 지나 입자의 개수가 일정 정도 수준을 유지하는 활성상태가 된다는 것을 알 수 있습니다. 더러운 임계점까지는 입자가 언젠가는 사라지고 다시는 생겨나지 않는 흡수상태로 끝납니다.
깨끗한 임계점(복제율이 약 3.3일 때)에서는 입자의 개수가 시간에 따라 줄어드는 건 펼쳐진 지수함수 모양이라고 했죠. 시각 t에 입자의 밀도를 ρ(t)라고 하면, 다음처럼 쓸 수 있다는 말이죠.
여기서 α가 1이면 그냥 '지수함수'인데 1이 아니면 '펼쳐진 지수함수(stretched exponential)'라고 합니다. 구체적으로 α = d / (d+z) 로 알려져 있습니다. d는 시스템의 공간차원, z는 이른바 동적 지수(dynamic exponent)이고 둘 다 알려져 있는데 여기서는 α가 약 0.3875입니다. 우리가 얻은 시늉내기 결과가 위 식을 만족시키는지 보려면 log ρ(t)가 t^0.3875와 비례하는지를 보면 됩니다. 아래 그림이 바로 그 결과입니다. 직선으로 보이는 부분이 있죠? 그 부분에서는 펼쳐진 지수함수 모양으로 입자의 개수가 감소하고 있다고 말할 수 있습니다.
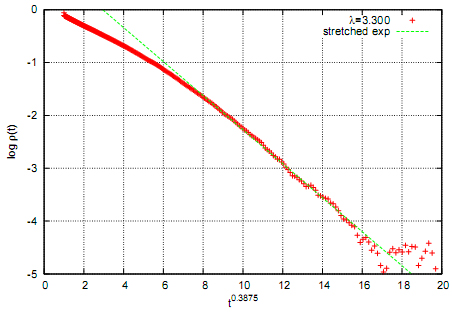
아래 그림은 그리피스 상태(복제율이 3.3보다 크고 5.0보다 작은 구간)에 대한 겁니다. 그리피스 상태에서도 입자는 계속 줄어들다가 사라져버리지만, 깨끗한 임계점에서와 달리 거듭제곱 꼴로 입자의 개수가 줄어듭니다. 그걸 확인하려면 log ρ(t)와 - log t가 비례하는 영역(즉 직선으로 보이는 영역)이 있는지 보면 됩니다. 보시면 있는 것 같죠? 그런데 그 직선의 기울기(즉 임계지수)가 복제율에 따라 다 다르게 나타나는 걸 알 수 있습니다. 이 임계지수는 복제율에 따라 연속적으로 변하는 것으로 보입니다.
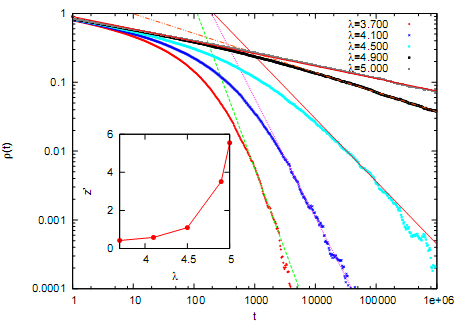
그림 안의 작은 그림에 복제율에 따른 지수의 변화를 그려넣었는데요, z'은 다음처럼 정의됩니다. 이런 정의는 관례에 따른(customarily used) 거라고 합니다.
아래 그림은 더러운 임계점 근처의 복제율들에 대해 누구나 동의하는 무한 무질서 고정점(IRFP)이 시늉내기로 확인되는지를 보인 겁니다. 보이타와 디키슨은 더러운 임계점이 약 5.24라고 하는데 제가 돌린 결과는 조금 달라서 5.0 근처로 기존 결과와 잘 맞는 것으로 보입니다.
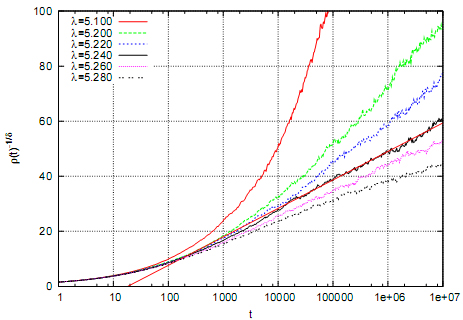
이론들은 여기서 다음과 같은 활성화된 눈금잡기(activated scaling)가 나타날 거라고 예상합니다.
이 예상이 잘 맞는지 보려면, 시늉내기 결과로부터 ρ^(-1/δ) 가 ln t와 비례하는지 보면 됩니다. 위 그림 중 맨 아래 그림이 그걸 그린 거고, 복제율이 5.24일 때 직선으로 보이는 부분이 잘 맞는 것으로 나타납니다.
(사실 이 정도로는 부족하고 4.95인지 5.03인지 소수점 아래 두세자리까지 보려면 좀더 세밀한 구간을 살펴봐야 합니다. 그런데 그러려면 시간이 너무 오래 걸립니다. 일단은 기존에 알려진 결과를 재현하는 정도가 목적이므로 이 정도만 했지만, 제대로 하려면 훨씬 더 많이, 더 오래, 더 자세히 돌려야 합니다.)
그런데 여기서 모호한 부분이 발견됩니다. 위의 가운데 그림, 즉 그리피스 상태의 결과 중에 복제율이 5.0인 것도 있었습니다. 여러 곡선 중 맨 위 곡선이 그것이죠. 거기서는 입자 개수의 변화가 거듭제곱 꼴일거라고 가정하고 쟀더니 기울기가 약 0.18이 나왔습니다. 거듭제곱 꼴이라고 가정해도 시늉내기 결과가 잘 맞는 것으로 보이고, 활성화된 눈금잡기라고 가정해도 역시 잘 맞는 것으로 보입니다. 하지만 '둘 다'라고 말할 수는 없죠.
어쨌든 보이타와 디키슨의 주장과 근거에 따르면, ln t는 시간이 매우 많이 흘러야만 확연히 나타나는데, 정말 시간이 많이 흐르고나면 거듭제곱보다는 활성화된 눈금잡기를 보여준다고 합니다.
점점 쓰기도 귀찮아지고, 시늉내기 결과에 대해 대충 할 얘기는 다 한 것 같고요, 그런데 왜 펼쳐진 지수함수, 활성화된 눈금잡기 같은게 나타나는지 설명을 안했는데요, 그건 수식이 필요하고, 그보다도 그 뒤에 깔려 있는 메커니즘 같은 걸 좀더 명쾌하게 이해하는 일이 남아있습니다. DCP에 관해서는 이 정도로 마치기로 하죠. 물론 제 기분 내키는대로 더 쓸 수도 있고 안 쓸 수도 있습니다.
위에 잠시 문제(?)가 되었던, 같은 결과인데 거듭제곱으로 볼거냐, 활성화된 눈금잡기로 볼거냐 하는 얘기가 있었죠. <알을 낳는 개>에서도 같은 결과인데 정반대의 해석을 가능하게 하는 '그림 그리기 테크닉'에 관한 이야기가 있습니다. 물론 그걸 이용해서 사기치라는 게 아니라 그걸 알아야 속지 않을 수 있다는 얘기입니다. 위에 그림을 두 가지 방식으로 그린 것도 사기까지는 아니지만, 충분히 보는 사람으로 하여금 혼란에 빠뜨릴 수 있습니다.
거듭제곱으로 그려놓고 거듭제곱이라고 주장해도 그런가보다 할 수 있고, 활성화된 눈금잡기로 그려놓고 그렇게 주장해도 그런가보다 할 수 있거든요. 보이타와 디키슨은 둘 다 그려놓고 '활성화된 눈금잡기'가 맞다고 주장하는데 이렇게 둘 다 그려보는 일이 필요합니다. 이미 그들의 결과가 있는데도 제가 다시 직접 돌려본 건 그걸 제 눈으로 확인하려는 것도 이유였습니다.
그런데 그들만큼 제대로 충분히 많이 돌리지 않아서 더러운 임계점도 좀 다르고(논문에서는 5.24, 저는 5.0), 이 글에 포함시키지는 않았지만 그들의 결과처럼 깔끔하게 나오지 않는 경우도 있어서 이 상태로는 그들의 결과를 검증/반증할만한 단계가 아닙니다. 그래서 여전히 '그런가보다'할 수밖에 없는 거죠.
그리고 무엇보다도 이렇게 오래 걸리는 시늉내기보다 좀더 직접적인 산수/수학을 통해 밝혀내는 일이 필요한데, 그러다보니 제가 할 수 있는 게 없더군요. 바로 이 지점에서 저는 컴퓨터로 계산이야 할 수 있지만 이론을 세울 능력이 없는 사람이 됩니다. 그럼 어떻게 해야 하느냐? 공부해야죠;;; 이제 자러 갑니다.
---
* 2008년 11월 24일 저녁 8시 20분 고침. 오늘 다시 보니 세 개의 그림 중 마지막 그림에 대해 틀리게 쓴 부분도 있고, 새로 얻은 결과도 있어서 일부 고쳤습니다. 어처구니 없는 실수를 해버렸네요. 세로축을 선형으로 그렸어야 했는데 로그로 그렸던 겁니다. 또한 이론으로 예측된 δ도 잘못 썼습니다. 그래서 다시 제대로 고쳤습니다.

